
Any examination of Frank Lloyd Wright’s homes leaves one with a feeling of transcendence. Wright’s strong, linear shapes and geometries imply a sense of order and artificiality. Yet these shapes evoke something deeper, something within nature.
Wright himself said that he was freed from the box. While simply breaking free from the basic box-like construction of a building does add a naturalness, to me it doesn’t finish the picture. There has always been something unique with his designs, and I believe he used his intuition to imitate the fractal nature of the world.
Cruciform, Weave and Additive
Paul Laseau and James Tice, authors of “Frank Lloyd Wright, Between Principle and Form” state on page 56:
Wright’s use of the cruciform suggests first and foremost a preference for a peculiar spacial “weaving” and a compositional preference for additive rather than subtractive plastic form… The cruciform house has both fluid movement and stability, change and continuity wrapped up in a form that enshrines the hearth, symbol of the family, and the four open arms that extend outward toward the landscape and toward freedom for the individual.
In this paragraph Laseau and Tice state three key words: cruciform, weaving and additive. They all have parallels in fractal design. I will investigate each further below.
Book can be purchased here.
The Cruciform is the Initiator
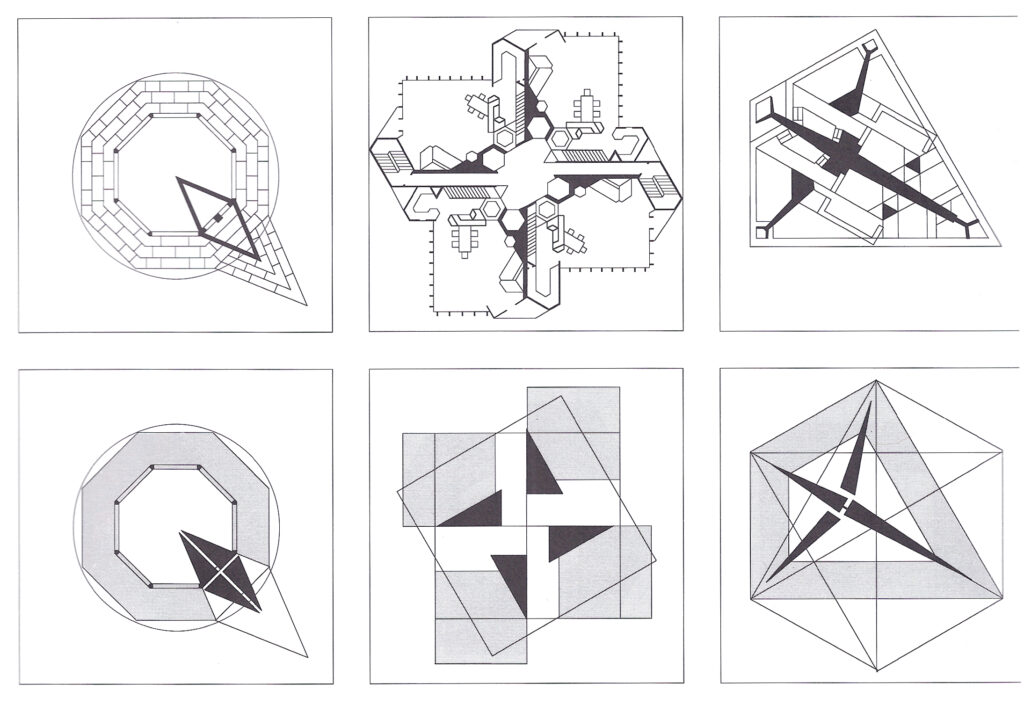
All fractals begin with what is called an Initiator. The initiator is the pattern that is repeated on an ever-diminishing scales. This is where one finds the famous “self-similarity of scale.
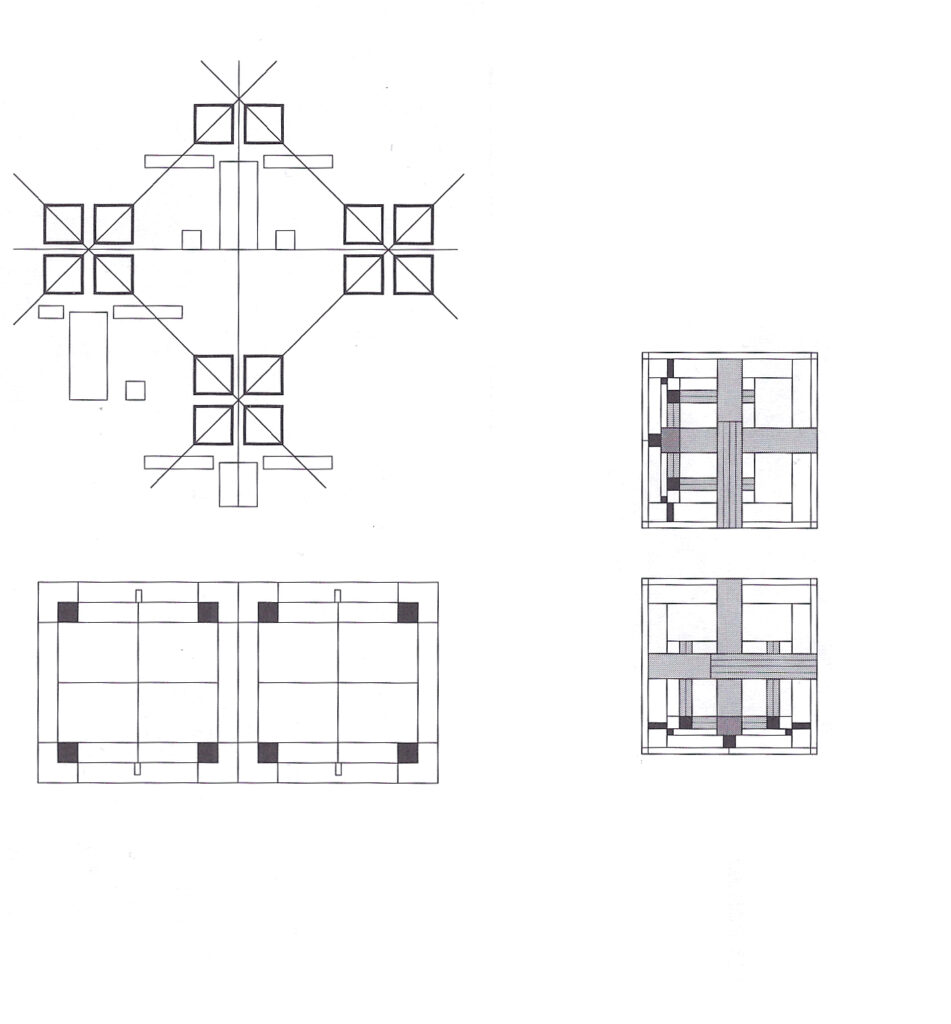
An example is the Koch Snowflake. One simply repeats the same pattern on an ever-decreasing scale. Below is an image taken from Benoit Mandelbrot’s book, “The Fractal Geometry of Nature.” (page 51) Book can be purchased here. The initiator in this case is a square that repeats endlessly and expands outward. As the pattern progresses, a definite image emerges. The main square, depending where it is placed, will create a pattern. (Where the square is placed is important and is explained below.)

Wright built many of his homes with the cruciform. The cruciform is the initiator. On page 52, Tice and Laseau state:
The cruciform plan and its transformations serve to inform almost all of Frank Lloyd Wright’s domestic work from the Prairie years to the Usonian House. The first accomplished building using this schema is the Willits House of 1902.
As an aside, Tice and Laseau mention that the cruciform did not originate with Wright, but was already a part of American vernacular housing. Bruce Price and Richardson had used the idea. It was also a part of Japanese design.
On page 55 they continue:
At [Jefferson’s] Monticello we can see precursors of Wright’s work in the embryonic cruciform, the asymmetrical distribution of the core, the hierarchical expression of the extending wings and the exaggerated extension of spaces into the landscape….Wright’s Willitts House can be seen as a further logical development of this theme of extended periphery and concomitant de-centering at the crossing.
And
In the Willitts, the corner volumes of the Blossom [house] that acted to buttress the internal space have been removed like form work to reveal the cruciform volumes they have molded.
And:
Although the cruciform has found complete expression in the Willitts House, the cubic volume is now implied rather than explicit. It is described by the outer edges of the living, dining and reception rooms.
Continuing:
Like the Rotunda (of Palladio), Willits has a strong concentric organization, but it is that of a solid that disintegrates with centrifugal force towards the four outstretched arms of the cruciform rather than the centripetal force that climaxes upward into the centralized dome.
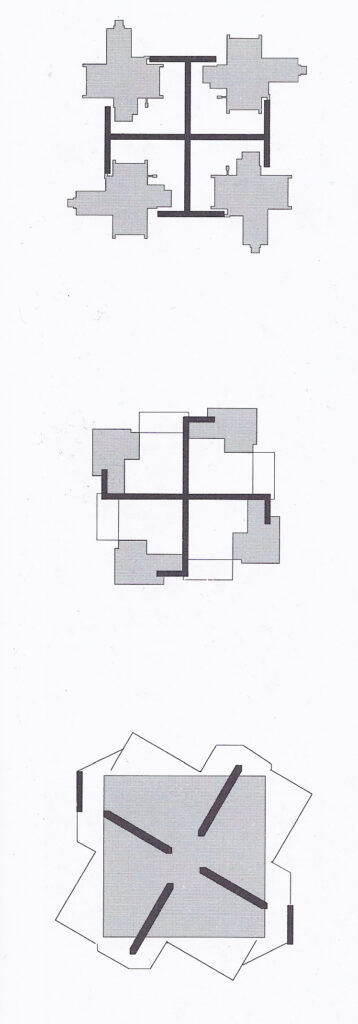
Below is a fractal that I created using a simple cruciform. I only placed the same cruciform in four places on each iteration. You can see that a strong, geometrical shape emerges from such a simple pattern.
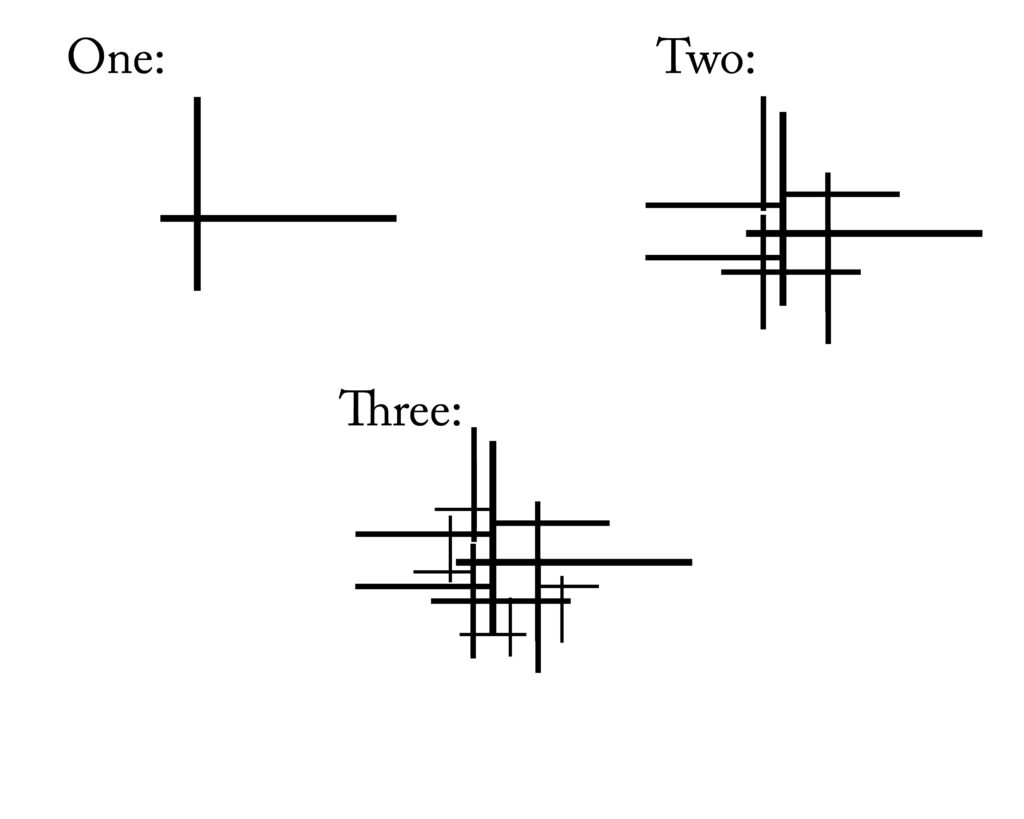
With a fractal, one can see that a fractal does indeed create a centrifugal force. Naturally, one has to modify the design for practical reasons. Concessions must be made. However, a sense of the cruciform expands outward and becomes part of the boundary.
The following plans show a fractal essence to Wright’s homes. All photos are taken from Laseau and Tice’s book, “Frank Lloyd Wright, Between Priniciple and Form.”
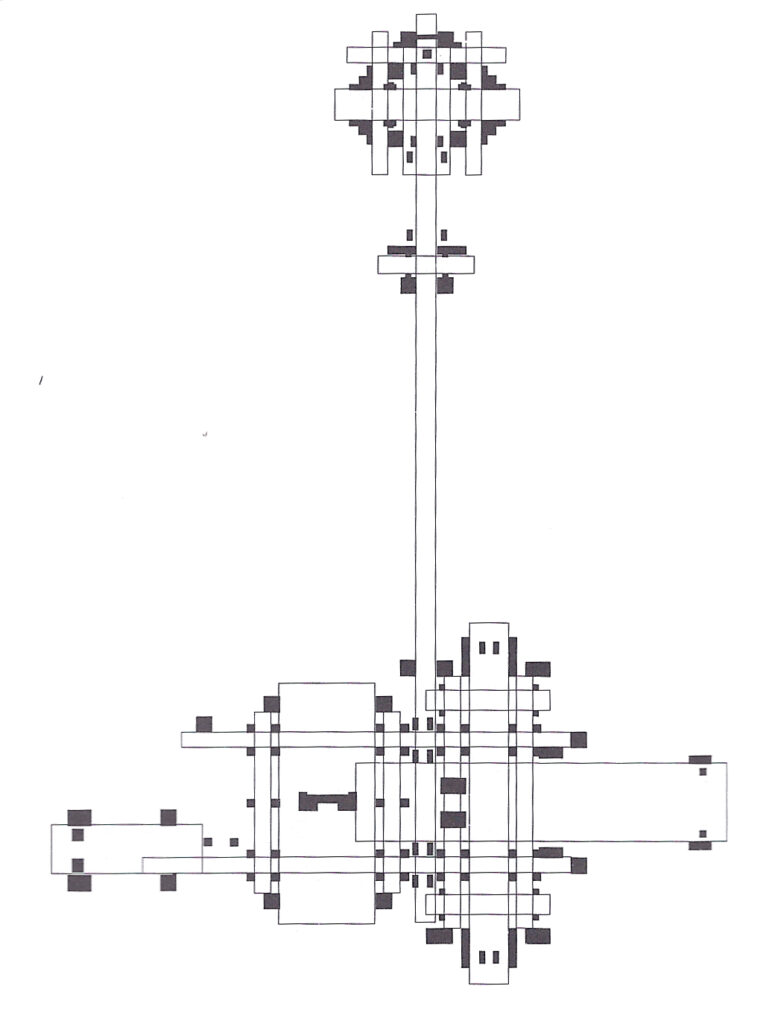
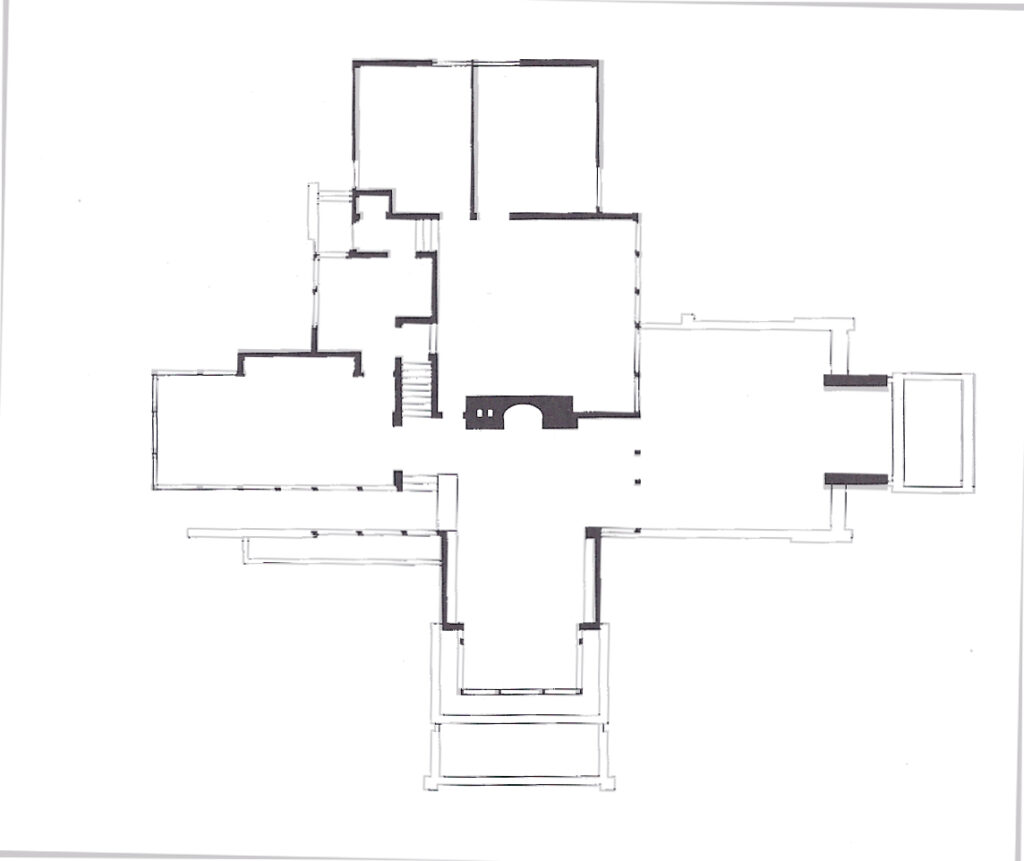
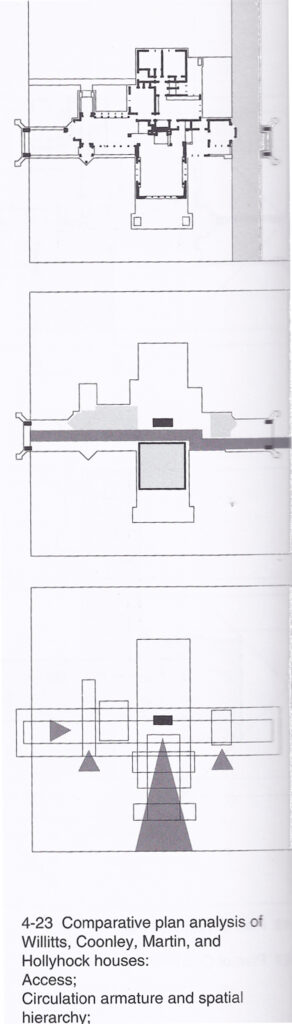
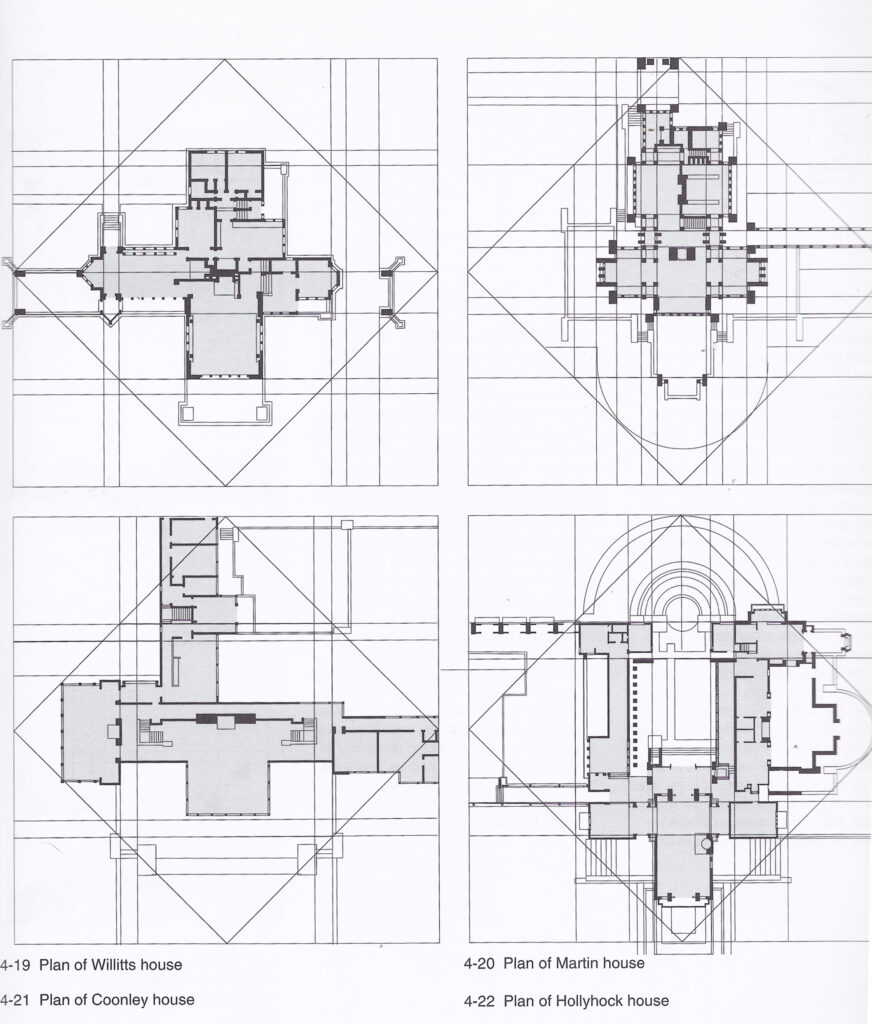
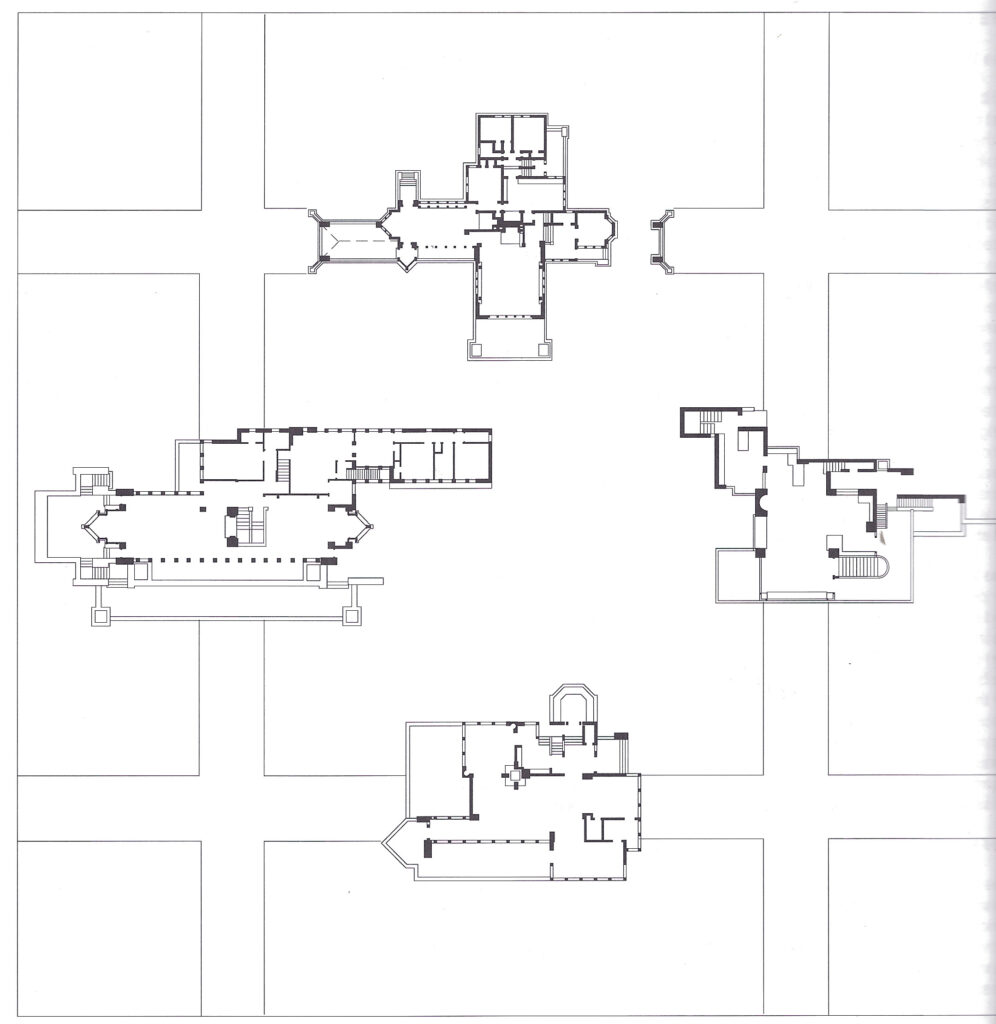
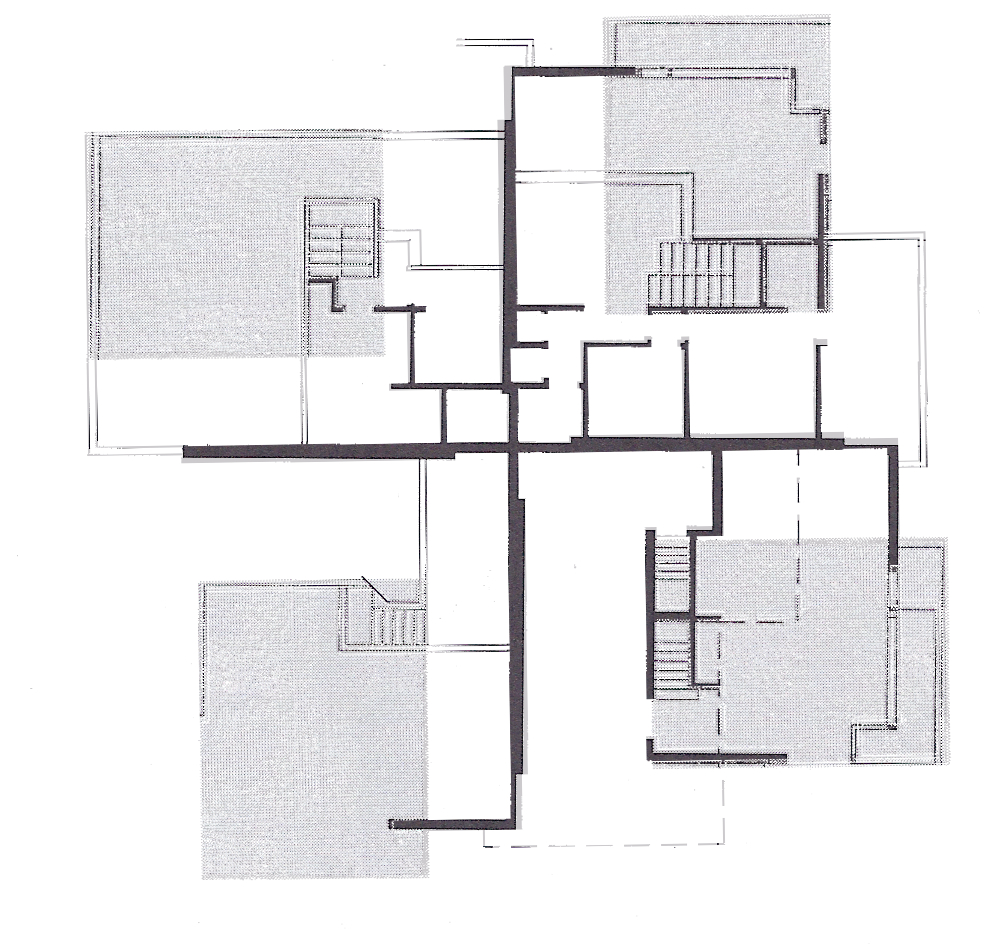
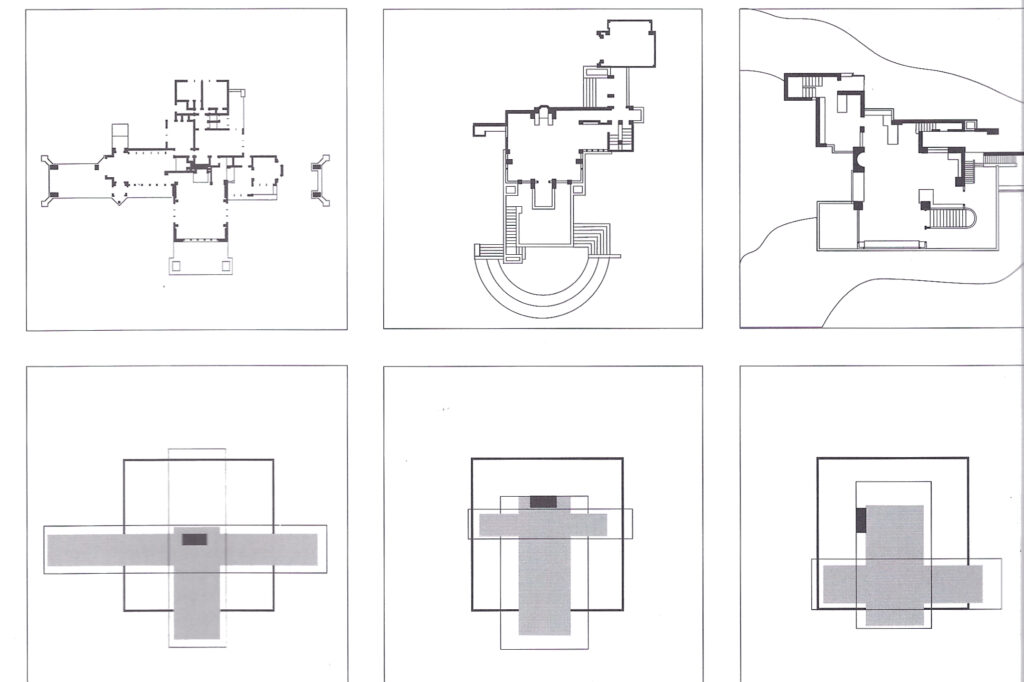
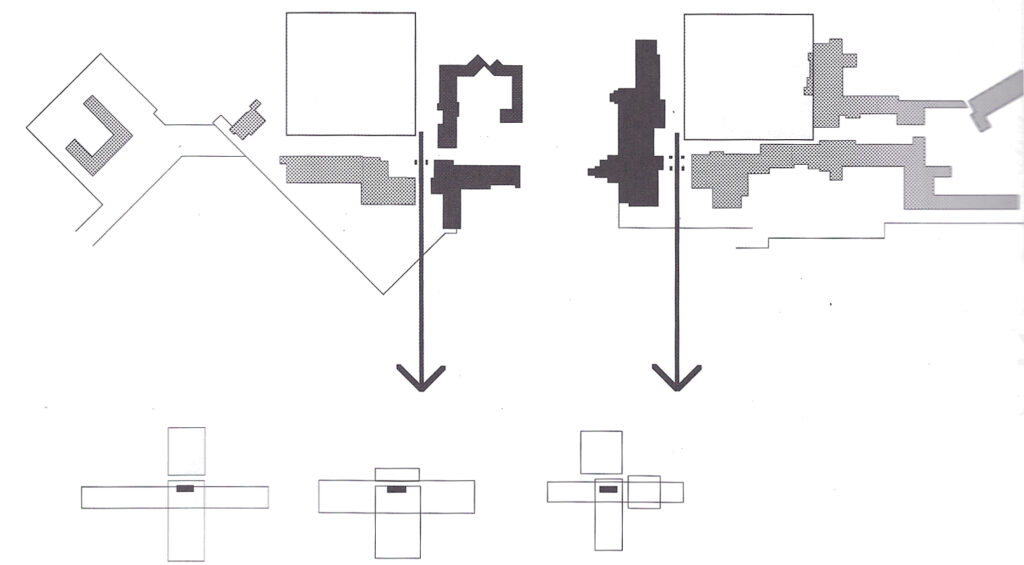
For further information on the initiator, Fractal Foundation can be helpful.
Weave
Weave can mean both a pattern (a weave) and a process (to weave.) Like a fractal, a weave must begin with one strand that interacts with another. All subsequent strands must build upon the original. The very nature of a woven object is that it is not a group of separate modules that can interact in simple, reductionistic ways. It is generated by iteration, by building upon what already exists.
The strands of a basket intertwine to create a solid, resilient shape. The strands interact with space, in fact, become a part of space. A cloud cannot be formed from blocks of clouds thrust together, or a mountain range is made from a juxtaposition of mounds of rock. These elements intertwine in a way that it looks as if they belong to nature, not that they are shoved into the landscape.
We see many thousands of different weaves. Anthropologists can define cultures by the weaving styles in baskets. Each is formed by repeating the same pattern.
A fractal is built the same way. It not only begins with a simple shape (square, triangle, cruciform for example) but how that shape is applied will create different fractals. Thus, just like a weaving pattern, we need a set of rules to define how this shape will build up.
In fractal geometry, one uses the generator. A fractal image begins with a number, it is manipulated by a set of rules, and a new number is created—which is plotted on the screen. That number is the input for the same set of rules, which then creates a new number (and plotted again.) This process repeats itself thousands of times. A picture emerges of self-similarity.
The following code comes from a Stack Overflow forum:
public void MBrot()
{
float epsilon = 0.0001; // The step size across the X and Y axis
float x;
float y;
int maxIterations = 10; // increasing this will give you a more detailed fractal
int maxColors = 256; // Change as appropriate for your display.
Complex Z;
Complex C;
int iterations;
for(x=-2; x<=2; x+= epsilon)
{
for(y=-2; y<=2; y+= epsilon)
{
iterations = 0;
C = new Complex(x, y);
Z = new Complex(0,0);
while(Complex.Abs(Z) < 2 && iterations < maxIterations)
{
Z = Z*Z + C;
iterations++;
}
Screen.Plot(x,y, maxColors % iterations); // depending on the number of iterations, color a pixel.
}
}
}There is no need to fully understand the steps of the program. The important point is to know that this simple set of rules is enough to create a fractal. The key is iteration, or taking the output and using it as the input for the next step.
Z = Z*Z + C;
Begin with a single number and build from there.
Additive
The finished product, after an initiator and a set of rules, is the fractal itself. Unlike modular shapes that can be arranged randomly, a fractal is additive. Its very nature is that it can only be generated from an initial shape and a governing process. We can say that it is additive.
One cannot pull apart a fractal and expect it to hold up any more than one can pull apart the strands of a basket and expect it to hold up.
Wright’s homes have the same sense of addition. Taking away any part of the home leaves a sense of incompleteness.
Finally, I’d like to add that although fractals can have a center, they often do not. As the fractal is concerned with the boundary of an object and not with the shape? Rather than the cruciform shape being enclosed by an outer box, the cruciform becomes the shape itself. Just as a fractal can have a definite shape, the boundaries are what defines the shape.
Wright home is often grasped by its boundaries. We see the cantilevers of Fallingwater and know immediately that it is a Wright home.’