Fractal Design incorporates new mathematical and physical ideas into design. For over a hundred years, mathematicians had struggled with strange functions that defied intuition and logic. (A function is an equation such as y = x+1.) In fact, they were called “monsters” because they didn’t behave predictably. Only since the 1960s have those functions, under the genius of Benoit Mandelbrot, become understandable. In 1975 he coined the word fractal, which comes from fragment. This makes sense because a fragment is a small part of a greater whole, which is what fractals are all about.
Meanwhile, scientists had been investigating natural processes such as the weather and turbulence that incorporated feedback. With the help of computers these scientists developed new means to imitate how nature operates. The overall term that describes this work can be called Chaos Theory.
Fractals and Chaos Theory are ideal for design inspiration because they are proving to be the basis of natural growth and form. We see them everywhere in nature. Of course, designers have incorporated many of these ideas intuitively over the millennia, for design cannot function unless it follows the rules of nature. What is different is explicitly using these new ideas in design.
Using the background above, we can divide Fractal Design into two parts. My hope is that this will change over time as the ideas evolve. Any comments or ideas are welcome. If you have anything you’d like to add, please contact me. My information is on the About Me page.
Fractals
A fractal is defined as exhibiting self-similarity of scale. A fractal can repeat itself as one examines it from a distance and up close. The most famous example of this is a coastline. The patterns of a coast look similar from a satellite and from someone walking along a beach and everywhere in between.
An important feature of a fractal is that it is not bound by the traditional 1, 2 or 3-dimensional Euclidean geometry. We say, for example, that a building has three dimensions: length, width and height. But a fractal doesn’t have one, two or three dimensions, but something in between. An example of this is the Koch Snowflake. Its dimension is 1.26. Also amazingly is that the line can be infinitely long!
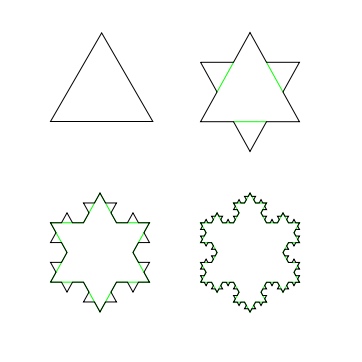
How can something be between dimensions and infinitely long? Lewis Fry Richardson studied the coastlines of many countries. He determined that there can never be a fixed coastline length because the smaller the measurement stick, the more detail you would measure and the longer the coastline would be. His insight was to determine that the dimension of a coast is not 1 or 2 dimensions, but somewhere in between. The smoother the coastline, the dimension becomes closer to 1. The more irregular, it gets closer to 2.
Mandelbrot took this idea and applied it to fractals. A two dimensional fractal will have a dimension between 1 and 2.
Chaos Theory and Strange Attractors
Chaos theory is a major field that is used in a large variety of disciplines such as physics, chemistry, biology and meteorology. The key element of this theory that will pertain to Fractal Design is the strange attractor.
A regular attractor (not strange) is best described by using a physical object such as a pendulum. As the pendulum swings back and forth, it makes an arc in 2 dimensional space. That is, it swings left and right, but also up and down. It also has a speed attached to it at every point. When the pendulum is hanging at its lowest point, it is traveling the fastest. When it is at its farthest and highest point it freezes for a brief moment.
For simplicity, we can ignore the height of the pendulum and only consider its distance to the left and right. Instead of the graph’s y-axis being a physical height, it will now be the pendulum’s speed. (Technically, this is called phase space and the object’s momentum is plotted, not its speed.) The graph that is formed turns into a circle. The extreme points of the x-axis will have zero speed, and the zero point of the x-axis will have the extreme speed. This circle repeats endlessly in a hypothetical environment, but because of air friction and other factors, the pendulum slows down and the oval will shrink over time until it ends in a point at the origin of the graph (point 0,0.)
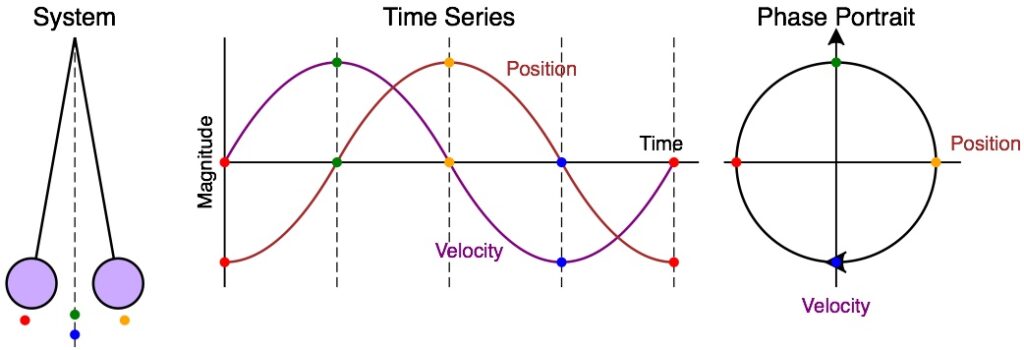
What scientists now have seen is that there are paths that never repeat. If you graph the infinite number of paths that some processes take, they will make a unique geometric object known as a strange attractor. All of the paths are unique, yet they congregate into a geometric form. Think of it as an object that is an encapsulation of all the ways a system can manifest over time.
And a strange attractor is a fractal. So it exhibits self-similarity of scale and will have a dimension that is not 1, 2, or 3, but something in between.
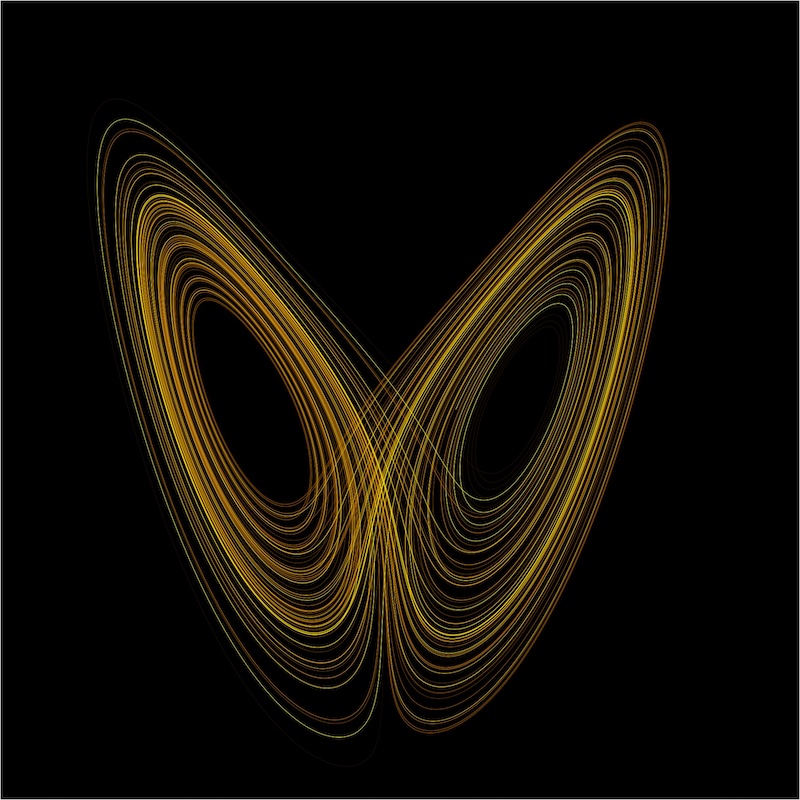
I am using a strange attractor as a basis for athroisis. The clustering of natural objects have a rough center around which these objects congregate. If you draw a line from each object, you will never have the same path.
We can incorporate these ideas into four principles of Fractal Design.
1) Athroisis (groupings) with subset of near symmetry
2) Iteration
3) Sensitive Dependence on Initial Conditions
4) Self Similarity.